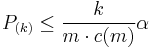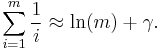False discovery rate
False discovery rate (FDR) control is a statistical method used in multiple hypothesis testing to correct for multiple comparisons. In a list of rejected hypotheses, FDR controls the expected proportion of incorrectly rejected null hypotheses (type I errors).[1] It is a less conservative procedure for comparison, with greater power than familywise error rate (FWER) control, at a cost of increasing the likelihood of obtaining type I errors.[2]
In practical terms, the FDR is the expected proportion of false positives among all significant hypotheses; for example, if 1000 observations were experimentally predicted to be different, and a maximum FDR for these observations was 0.10, then 100 of these observations would be expected to be false positives.
The q-value is defined to be the FDR analogue of the p-value. The q-value of an individual hypothesis test is the minimum FDR at which the test may be called significant. One approach is to directly estimate q-values rather than fixing a level at which to control the FDR.
Contents |
Classification of m hypothesis tests
The following table defines some random variables related to  hypothesis tests.
hypothesis tests.
| Null hypothesis is True (H0) | Alternative hypothesis is True (H1) | Total | |
|---|---|---|---|
| Declared significant |  |
 |
 |
| Declared non-significant |  |
 |
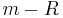 |
| Total | 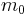 |
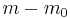 |
 |
 is the total number hypotheses tested
is the total number hypotheses tested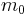 is the number of true null hypotheses
is the number of true null hypotheses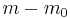 is the number of true alternative hypotheses
is the number of true alternative hypotheses is the number of false positives (Type I error)
is the number of false positives (Type I error) is the number of true positives
is the number of true positives is the number of false negatives (Type II error)
is the number of false negatives (Type II error) is the number of true negatives
is the number of true negatives
- In
 hypothesis tests of which
hypothesis tests of which 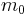 are true null hypotheses,
are true null hypotheses,  is an observable random variable, and
is an observable random variable, and  ,
,  ,
,  , and
, and  are unobservable random variables.
are unobservable random variables.
The false discovery rate is given by ![\mathrm{E}\!\left [\frac{V}{V%2BS}\right ] = \mathrm{E}\!\left [\frac{V}{R}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/abc64f9554aa7c896ffb177791f10a9c.png) and one wants to keep this value below a threshold
and one wants to keep this value below a threshold  .
.
(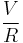 is defined to be 0 when
is defined to be 0 when  )
)
History
By the 1980s and 1990s, advanced technology had made it possible to perform hundreds and thousands of statistical tests on a given data set. In this environment, traditional multiple comparison procedures began to appear as too conservative. The False Discovery Rate concept was formally described by Benjamini and Hochberg (1995)[1] as a less conservative and arguably more appropriate approach for identifying the important few from the trivial many effects tested. Efron and others have since connected it to the literature on Empirical Bayes.[3].
The growth of methodology for multiple hypothesis testing in recent times is closely tied the development of “high-throughput” science. With the advent of technology for rapid data acquisition, it became possible to perform statistical tests on hundreds or thousands of features from a single dataset. The technology of microarrays was a prototypical example, as it enabled thousands of genes to be tested simultaneously for differential expression between two biological conditions. As high-throughput technologies became common- place, the drawbacks to FWER and unadjusted multiple hypothesis testing became more widely known in many scientific communities. In response to this development, a variety of error rates have been proposed to offer a more flexible tradeoff between power and error. Among these different notions of error, the FDR (Benjamini and Hochberg 1995, ) has been particularly influential, as it was the first alternative to the FWER to gain broad acceptance in many scientific fields.
Prior to the 1995 introduction of the FDR concept, various precursor ideas had been considered in the statistics literature. In 1979, Holm proposed a stepwise algorithm for controlling the FWER that is at least as powerful as the well-known Bonferroni adjustment. This stepwise algorithm sorts the p-values and sequentially rejects the hypotheses starting from the smallest p-value (see Efron 3.3 for details). In a 1982 paper, Schweder and Spjotvoll noted that by plotting sorted p-values, those p-values corresponding to the true null hypotheses should form a straight line starting from the largest p-values. The p-values that deviate from this straight line then should correspond to the false null hypotheses. This idea is closely related to the graphical interpretation of the BH procedure. The terminology of “discovery” in the multiple hypothesis testing context was introduced in a 1989 paper of Soric, who called attention to the probability of making a false rejection given that a rejection has been made–which is related to the false discovery proportion considered by Benjamini and Hochberg.
Controlling procedures
Independent tests
The Simes procedure ensures that its expected value ![\mathrm{E}\!\left[ \frac{V}{V %2B S} \right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/3d00cc1bfede820163bea7a31d5e66e8.png) is less than a given
is less than a given  [1]. This procedure is valid when the
[1]. This procedure is valid when the  tests are independent. Let
tests are independent. Let  be the null hypotheses and
be the null hypotheses and  their corresponding p-values. Order these values in increasing order and denote them by
their corresponding p-values. Order these values in increasing order and denote them by  . For a given
. For a given  , find the largest
, find the largest  such that
such that 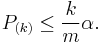
Then reject (i.e. declare positive) all 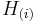 for
for 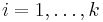 .
.
Note that the mean  for these
for these  tests is
tests is 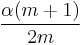 which could be used as a rough FDR, or RFDR, "
which could be used as a rough FDR, or RFDR, " adjusted for
adjusted for  independent (or positively correlated, see below) tests." The RFDR calculation shown here provides a useful approximation and is not part of the Benjamini and Hochberg method; see AFDR below.
independent (or positively correlated, see below) tests." The RFDR calculation shown here provides a useful approximation and is not part of the Benjamini and Hochberg method; see AFDR below.
Dependent tests
The Benjamini–Hochberg–Yekutieli procedure controls the false discovery rate under dependence assumptions. This refinement modifies the threshold and finds the largest k such that:
- If the tests are independent: c(m) = 1 (same as above)
- If the tests are positively correlated: c(m) = 1
- Under arbitrary dependence:
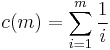
In the case of negative correlation, 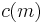 can be approximated by using the Euler–Mascheroni constant.
can be approximated by using the Euler–Mascheroni constant.
Using RFDR above, an approximate FDR, or AFDR, is the min(mean α) for m tests = RFDR / ( ln(m) + 0.57721...).
Large-Scale Inference
Let 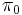 be the probability that the null hypothesis is correct, and
be the probability that the null hypothesis is correct, and 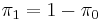 be the probability that the alternative is correct. Then
be the probability that the alternative is correct. Then 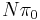 times the average p-value of rejected effects divided by the number of rejected effects gives an estimate of the FDR. While we do not know
times the average p-value of rejected effects divided by the number of rejected effects gives an estimate of the FDR. While we do not know 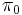 , it is typically close enough to 1 that we can get a reasonable estimate of the FDR by assuming it is 1. This and many related results are discussed in Efron (2010).[3]
, it is typically close enough to 1 that we can get a reasonable estimate of the FDR by assuming it is 1. This and many related results are discussed in Efron (2010).[3]
References
- ^ a b c Benjamini, Yoav; Hochberg, Yosef (1995). "Controlling the false discovery rate: a practical and powerful approach to multiple testing". Journal of the Royal Statistical Society, Series B (Methodological) 57 (1): 289–300. MR1325392. http://www.math.tau.ac.il/~ybenja/MyPapers/benjamini_hochberg1995.pdf.
- ^ Shaffer J.P. (1995) Multiple hypothesis testing, Annual Review of Psychology 46:561-584, Annual Reviews
- ^ a b Efron, Bradley (2010). Large-Scale Inference. Cambridge University Press. ISBN 978-0-521-19249.
Further Reading
- Benjamini, Yoav; Yekutieli, Daniel (2001). "The control of the false discovery rate in multiple testing under dependency". Annals of Statistics 29 (4): 1165–1188. doi:10.1214/aos/1013699998. MR1869245. http://www.math.tau.ac.il/~ybenja/MyPapers/benjamini_yekutieli_ANNSTAT2001.pdf.
- Storey, John D. (2002). "A direct approach to false discovery rates". Journal of the Royal Statistical Society, Series B (Methodological) 64 (3): 479–498. doi:10.1111/1467-9868.00346. MR1924302. http://www.blackwell-synergy.com/links/doi/10.1111%2F1467-9868.00346.
- Storey, John D. (2003). "The positive false discovery rate: A Bayesian interpretation and the q-value". Annals of Statistics 31 (6): 2013–2035. doi:10.1214/aos/1074290335. MR2036398. http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.aos/1074290335.
External links
- False Discovery Rate Analysis in R – Lists links with popular R packages